Hunting for "riftrunner" on LMArena: Gemini 3.0 Rumor + Battle Derivation

Rumor: Gemini 3.0 is hiding on LMArena under the codename riftrunner. I camped in Battle mode until riftrunner appeared, then threw a calculus recurrence at it to see how it reasons.

Why this matters

• LMArena sometimes ships experimental models under code names.


• Reports say riftrunner is stronger at stepwise math derivations.


• If true, this could be an early look at Gemini 3.0's reasoning upgrades.

What I did

1. Stayed in Battle until the right-hand side showed riftrunner.


2. Prompted both sides with the same integral recurrence to stress symbolic reasoning.


3. Judged on derivation steps and algebra hygiene, not just final values.

The problem (reduction formula)

Show that for I_n = \int_{0}^{\pi/2} x \cos^n x \, dx:

I_n = ((n-1)/n) I_{n-2} - 1/n^2

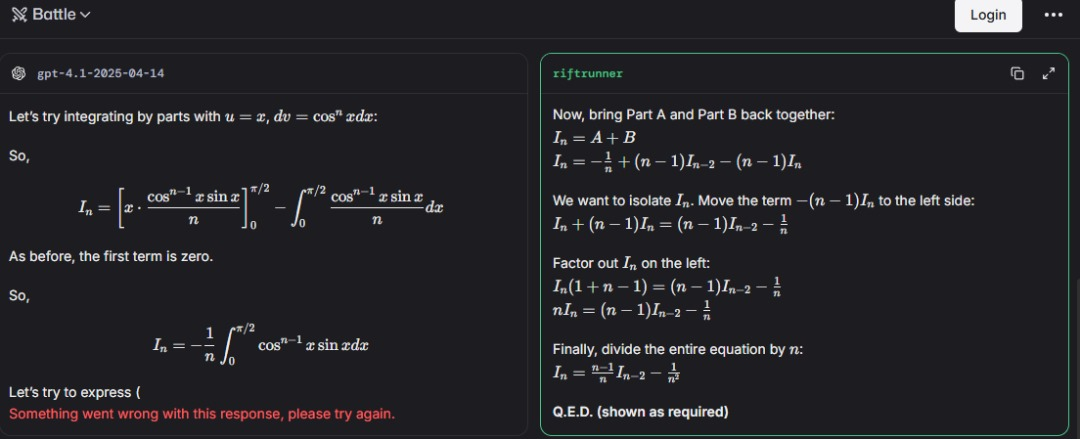
How riftrunner solved it (key moves)

1. Integration by parts with u = x, dv = \cos^n x\,dx; boundary term is 0, leaving -(1/n) \int_{0}^{\pi/2} x \cos^{n-1}x \sin x \, dx.


2. Split the remaining integral: one part factors out x for recurrence, the other rewrites \cos^{n-1}x in terms of I_{n-2} after differentiation.


3. Combine to get I_n = -(1/n) + (n-1)I_{n-2} - (n-1)I_n.


4. Group like terms: I_n + (n-1)I_n = (n-1)I_{n-2} - 1/n.


5. Divide by n: I_n = ((n-1)/n) I_{n-2} - 1/n^2. Done.

What felt different about riftrunner

• Clean factor handling: pulled I_n to one side before dividing, avoiding sign slips.


• Fewer dead ends: minimal backtracking vs. other models that stalled mid-derivation.


• Textbook finish: concise recurrence and tidy Q.E.D.-style wrap.

Takeaways

This small Battle-mode trial hints that riftrunner—if it’s really Gemini 3.0—has tighter symbolic reasoning. To replicate, wait for riftrunner in Battle, then test tougher integrals or series proofs to see if the edge holds.